高频算法三十讲

一、反转链表

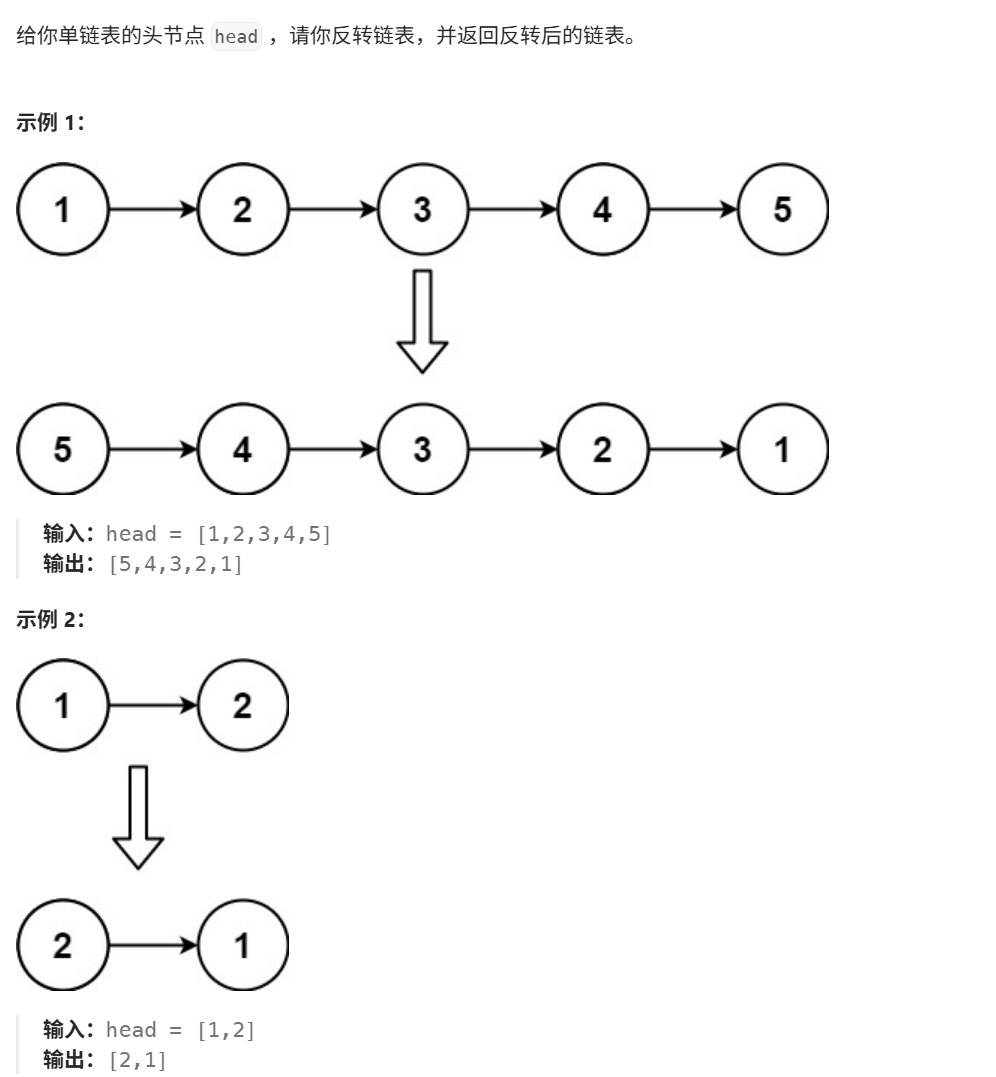
image-20250502140048797

思路：定义三个节点指针，cur，tmp，pre。断后，连前，移节点。

cur：指向头节点

tmp：指向头节点的下一节点

pre：方向节点

以cur断开原本next，从而指向pre方向，再向前移动pr和cur实现方向反转。

  1. tmp=cur->next;

    tmp始终都在cur后面，以方便后面cur移动节点

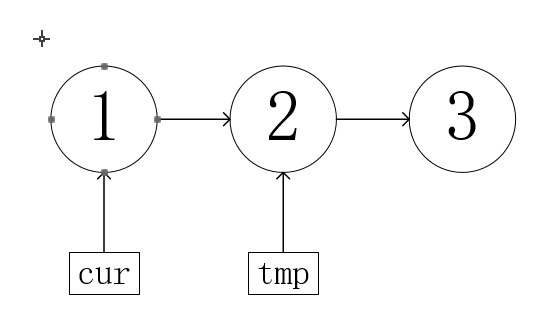
image-20250502140805635

  1. cur->next=pre;

    改变链表方向

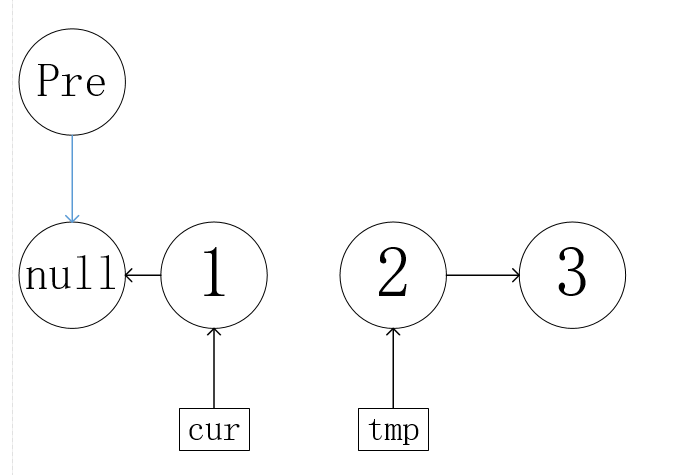
    image-20250502141406674

    1. pre=cur; cur=tmp;

      节点移动

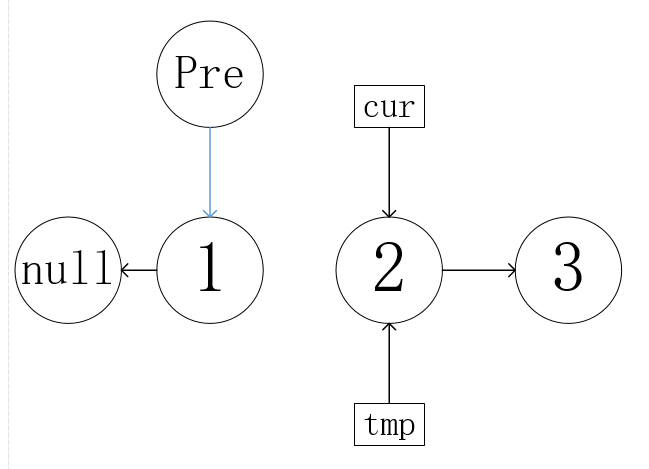
      image-20250502141608073

      1. while循环遍历直到cur为null。

二、轮转数组

image-20250502151242597 
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int n=nums.size();
        vector<int> numArry(n);
        for(int i=0;i<n;i++)
        {
            numArry[(i+k)%n]=nums[i];
        }
        nums.assign(numArry.begin(),numArry.end());//assign()将一个容器内的元素按照特定规则赋值到另一个容器中
    }
};

关键公式：(i+k)%n 轮转后索引=(当前索引+轮转步数)%数组大小

三、两数之和

image-20250502152003783

思路：哈希表，遍历数组，用target减去遍历的值去找哈希表。在就返回不在就入表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int> hashtable;
        for(int i=0;i<nums.size();i++)
        {
            auto it=hashtable.find(target - nums[i]);
            if(it!=hashtable.end())
            {
                return {it->second,i};
            }
             hashtable[nums[i]] =i ;
        }
       
        return {};
    }
};

四、有效的括号

image-20250502231917652

思路：用字典来判断匹配括号，用进出栈的顺序来判断是否为对应括号。如果栈顶元素和字典对应元素相等为匹配成功

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    bool isValid(string s) {
//
        if(s.size()%2!=0){
            return false;//如果输入的括号不是偶数直接返回错误
        }
         
         unordered_map<char,char> dic={
           {')','('},
           {'}','{'},
           {']','['}
         };
        stack<char> stk;
        for(char ch:s)//遍历字符串或列表
        {
            if(dic.count(ch))//如果在表内直接接入
         {
             if(stk.empty()||stk.top()!=dic[ch])//如果栈是空的，或者另一半对不上，直接返回错误
             {
                    return false; //栈空说明，没有左半括号
             }
             else
             {
                   stk.pop();//匹配成功出栈
             }
         }
          else 
         {
                stk.push(ch);//不再表内的压入栈
         }
        } 
         return stk.empty();
    }   
};

五、每日温度

image-20250503104918417

思路：单调栈

1.什么是单调栈

单调栈是一个有序的栈，可能从栈顶到栈底单调递增（单调递增栈），也有可能从栈顶到栈底单调递减（单调递减栈）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
stack<int> st;
//此处一般需要给数组最后添加结束标志符，具体下面例题会有详细讲解
for (遍历这个数组)
{
	if (栈空 || 栈顶元素大于等于当前比较元素)
	{
		入栈;
	}
	else
	{
		while (栈不为空 && 栈顶元素小于当前元素)
		{
			栈顶元素出栈;
			更新结果;
		}
		当前数据入栈;
	}
}

题解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        int n=temperatures.size();
        vector<int> answer(n);//新建数组返回答案
        stack<int> s;
        for(int i=0;i<n;i++){//遍历整个数组
            while(!s.empty()&&temperatures[i]>temperatures[s.top()])//用单调栈，这里栈顶元素是天数，把天数压入
            {
                answer[s.top()]=i-s.top();
                s.pop();
            }
            s.push(i);
        }
        return answer;
    }
};

六、二叉搜索树中第 K 小的元素

1.前序遍历

1.访问根节点；2.访问当前节点的左子树；3.若当前节点无左子树，则访问当前节点的右子树；即考察到一个节点后，即刻输出该节点的值，并继续遍历其左右子树。(根左右)

因为要在遍历完某个树的根节点的左子树后接着遍历节点的右子树，为了能找到该树的根节点，需要使用栈来进行暂存。中序和后序也都涉及到回溯，所以都需要用到栈。

img

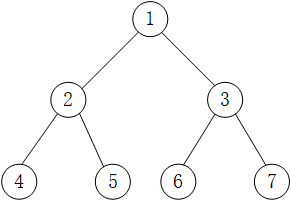
图 中二叉树采用先序遍历得到的序列为：1 2 4 5 3 6 7

2. 中序遍历

二叉树中序遍历的实现思想是：1.访问当前节点的左子树；2.访问根节点；3.访问当前节点的右子树。即考察到一个节点后，将其暂存，遍历完左子树后，再输出该节点的值，然后遍历右子树。(左根右)

img

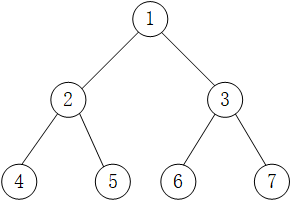
上图中二叉树采用中序遍历得到的序列为：4 2 5 1 6 3 7

3. 后序遍历

二叉树后序遍历的实现思想是：1.访问左子树；2.访问右子树；3.完成该节点的左右子树的访问后，再访问该节点。即考察到一个节点后，将其暂存，遍历完左右子树后，再输出该节点的值。(左右根)

img

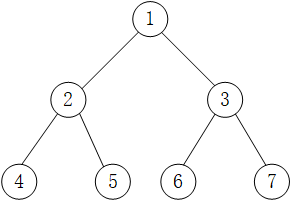
对上图 中二叉树进行后序遍历的结果为：4 5 2 6 7 3 1

4.题目

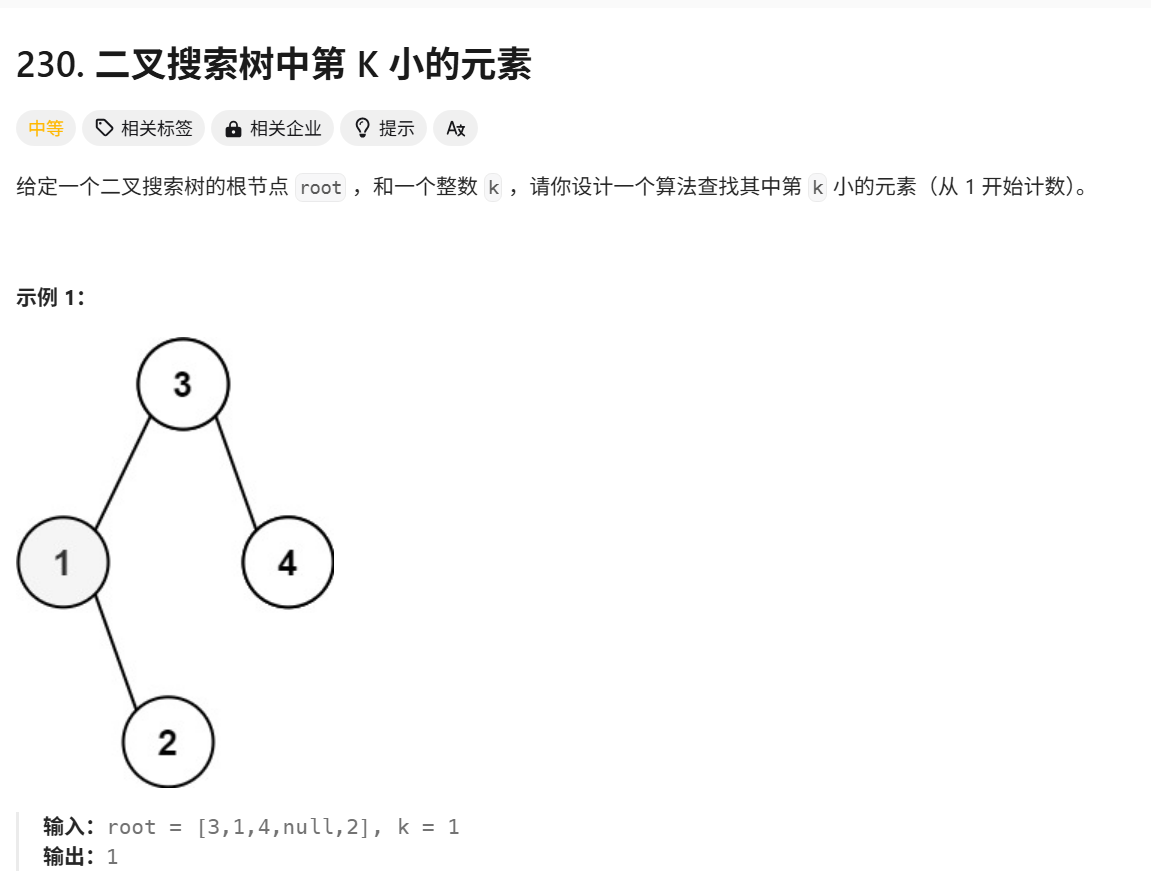
image-20250503125544887

思路：因为左树都是比节点小，所以优先使中序遍历；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        stack<TreeNode*> stk;
        while(root!=nullptr||stk.size()>0){
            while(root!=nullptr){
                stk.push(root);
                root=root->left;
            }
            root=stk.top();
            stk.pop();
            k--;
            if(k==0)
            {
                break;
            }
            else{
                root=root->right;
            }

        }   
        return root->val;
    }
};

七、求根节点到叶节点数字之和

1.深度优先遍历

一种用于遍历或搜索树或图的算法。 沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过或者在搜寻时结点不满足条件，搜索将回溯到发现节点v的那条边的起始节点。整个进程反复进行直到所有节点都被访问为止。属于盲目搜索,最糟糕的情况算法时间复杂度为O(！n)。

2.题目

image-20250503134613033

思路：遇到树或者图，就想递归处理或者前中后遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int sumNumbers(TreeNode* root) {
        return dfs(root,0);
    }
    int dfs(TreeNode* root,int prenum){
        if(root==nullptr)
          return 0;
        int sum=prenum*10+root->val;
        if(root->left==nullptr&&root->right==nullptr)
        {
            return sum;
        }else{
            return dfs(root->left,sum)+dfs(root->right,sum);
        }
    }
};

八、