Unity之Mesh网格
引言:
- 本笔记为各方资料整理,如有侵权请联系
创建一个简单的网格
渲染事物
在 Unity 中,如果你想将某些内容可视化,可以使用网格。它可以是从其他程序导出的 3D 模型,也可以是程序生成的网格,还可以是精灵图、UI 元素或粒子系统,这些 Unity 也使用网格来实现。甚至屏幕效果也使用网格进行渲染。
那么,什么是网格??
一组3D空间点+一组连接点的三角形(这些三角形构成了网格所代表内容的表面。)
由于三角形是
平面的,且边缘笔直,因此它们可以用来完美地呈现平面和直线的物体,例如立方体的面。曲面或圆形表面只能通过使用许多小三角形来近似。如果三角形看起来足够小(不大于一个像素),那么您将无法察觉到这种近似。通常,这对于实时性能来说是不可行的,因此表面总会呈现出某种程度的锯齿状。

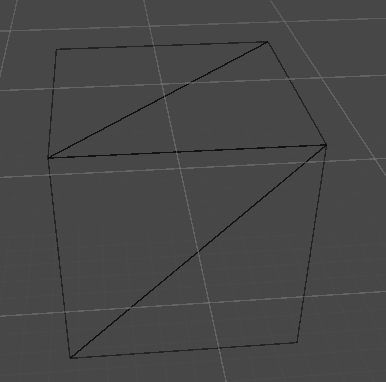
图1 Unity默认立方体以及线宽(能看到锯齿)
如何显示线框?您可以在场景视图的左侧工具栏中选择其显示模式。前三个选项分别是“Shaded”(阴影)、“Wireframe”(线框)和“Shaded Wireframe”(阴影线框)。
如何显示3D模型?它需要两个组件。
- 第一个是
网格过滤器。该组件保存对要显示的网格的引用。- 第二个是
网格渲染器。使用它来配置网格的渲染方式,例如使用哪种材质、是否投射或接收阴影等等。
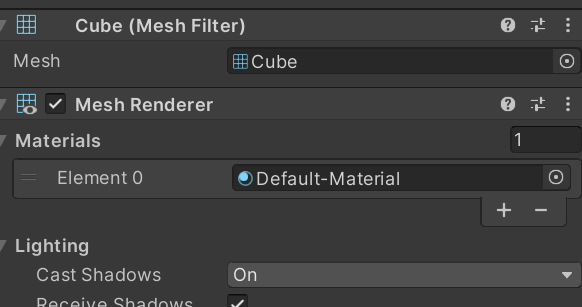
图2 网格过滤器和渲染器
| 为什么网格渲染器里面可以添加一系列的材质??? |
|---|
网格渲染器可以拥有多种材质。这主要用于渲染包含多个独立三角形集(称为子网格)的网格。 |
您可以通过调整网格的材质来彻底改变其外观。Unity 的默认材质是纯白色。您可以通过*“Assets / Create / Material”*创建新的材质资源并将其拖到游戏对象上,将其替换为您自己的材质。新材质默认使用 Unity 的标准着色器,该着色器为您提供了一组控件来调整表面的视觉效果。
为网格添加大量细节的一种快速方法是提供反照率贴图。反照率贴图是一张表示材质基本颜色的纹理。当然,我们需要知道如何将此纹理投影到网格的三角形上。这可以通过向顶点添加二维纹理坐标来实现。纹理空间的两个维度称为U和V,这就是它们被称为 UV 坐标的原因。这些坐标通常位于**(0, 0)和(1, 1)**之间,覆盖整个纹理。根据纹理设置,超出该范围的坐标要么被限制,要么导致平铺。
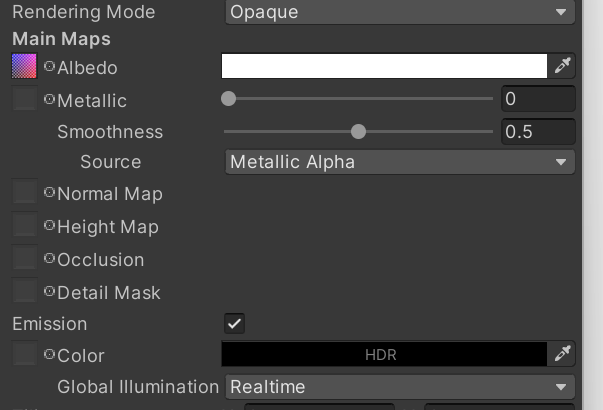

图3 Unity的UV测试网格
创建顶点网格
让我们先来了解一下,先生成一个简单的矩形网格。该网格由单位长度的正方形图块(四边形)组成。创建一个新的 C# 脚本,并将其转换为具有水平和垂直尺寸的网格组件。
1 | using System.Collections; |
当我们将此组件添加到游戏对象时,我们还需要
为其添加网格过滤器和网格渲染器。我们可以在类中添加一个属性,让 Unity 自动添加它们。
1 | [] |
现在,您可以创建一个新的空游戏对象,并向其中添加网格组件,这样它就包含另外两个组件了。
设置渲染器的材质,并保留滤镜的网格。我将网格的尺寸设置为 10 x 5。
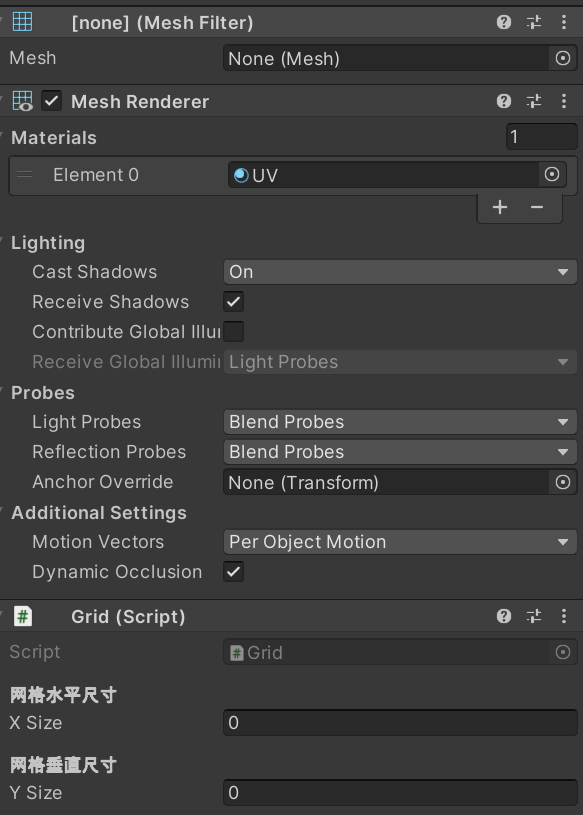
图4 网格对象
一旦对象被唤醒,我们就会生成实际的网格.
1 | private void Awake() |
我们先关注顶点位置,三角形留到以后再说。
我们需要一个
3D 矢量数组来存储这些点。顶点的数量取决于网格的大小。
每个四边形的角上都需要一个顶点,但相邻的四边形可以共享同一个顶点。因此,我们
需要的顶点数量比每个维度上的图块数量多一个。水平顶点数(x+1) 垂直顶点数(y+1)
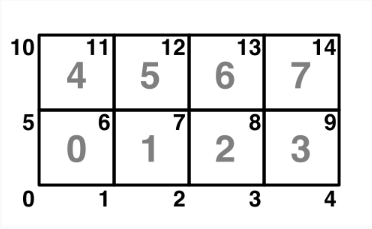
图5 4X2网格示例和四边形索引
让我们将这些顶点可视化,以便检查它们的位置是否正确。我们可以添加一个
OnDrawGizmos方法,并在场景视图中为每个顶点绘制一个小黑球。
| 什么是Gizmo |
|---|
Gizmo 是您可以在编辑器中使用的视觉提示。默认情况下,它们在场景视图中可见,在游戏视图中不可见,但您可以通过其工具栏进行调整。Gizmos工具类允许您绘制图标、线条和其他一些内容。 |
当我们不在运行模式时,这会产生错误,因为
OnDrawGizmos当 Unity 处于编辑模式时,即使我们没有任何顶点,也会调用方法。为了避免此错误,请检查数组是否存在,如果不存在,则跳出该方法。
1 | private void OnDrawGizmos() |

图6 绘制的顶点
此时所有的顶点默认都是原点位置,所以我们要在 Generate();函数中将位置重新赋值
1 | private void Generate() |

图7 网格顶点绘制完毕
| 为什么小黑点不会随着物体移动???? |
|---|
| Gizmo直接在世界空间中绘制,而不是在对象的局部坐标空间中绘制。如果希望它们遵循对象的变换,则必须使用transform.TransformPoint(vertices[i])。 |
现在我们可以看到顶点了,但它们的放置顺序却不可见。我们可以用颜色来显示,也可以使用协程来减慢这个过程。这就是我把它添加
using System.Collections到脚本中的原因。
1 | private void Awake() |
图8 顶点顺序绘制
创建网格
现在我们知道顶点的位置正确了,我们就可以处理实际的网格了。除了在我们自己的组件中保存对它的引用之外,我们还必须将其赋值给网格过滤器。处理完顶点后,我们就可以将它们赋值给网格了。
1 | private Mesh mesh; |

图8 运行时出现网格
现在,我们在播放模式下已经有了一个网格,但它还没有显示出来,因为我们还没有给它分配任何三角形。
三角形是通过
顶点索引数组定义的。由于每个三角形有三个点,所以
三个连续的索引可以描述一个三角形。让我们先从一个三角形开始。
1 | private IEnumerator Generate () { |
我们现在有一个三角形,但我们使用的三个点都在一条直线上。这会产生一个退化的三角形,不可见。前两个顶点没有问题,但我们应该跳到下一行的第一个顶点。
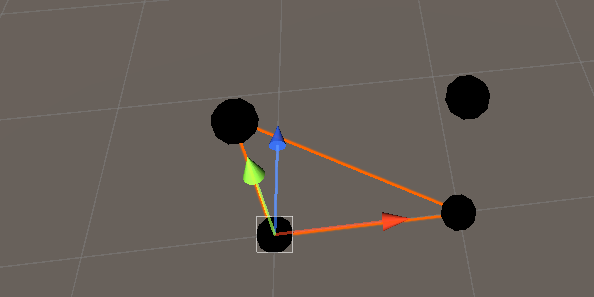
图9 绘制三角形(反)
1 | triangles[0] = 0; |
这确实给出了一个三角形,但它只能从一个方向可见。在这种情况下,只有从 Z 轴的反方向看时才可见。
所以你可能需要旋转视图才能看到它。
三角形从哪一侧可见取决于其顶点索引的方向。
默认情况下,如果它们按顺时针方向排列,则该三角形被视为朝前且可见。逆时针方向的三角形会被丢弃,这样我们就不需要花时间渲染物体的内部,因为通常情况下,物体的内部是不应该被看到的。
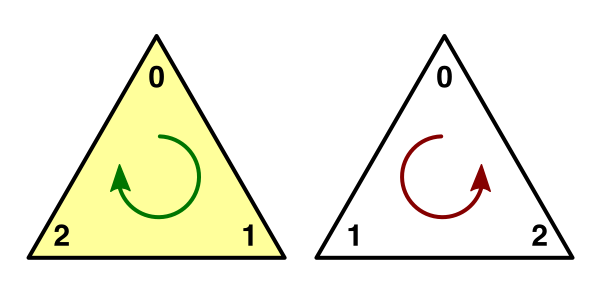
图10 三角形索引顺序
因此,为了让三角形在 Z 轴方向上可见,我们必须改变顶点的遍历顺序。我们可以通过交换最后两个索引来实现。
1 | triangles[0] = 0; |

图11 第一个三角形
现在,我们已经有一个三角形覆盖了网格第一个图块的一半。要覆盖整个图块,我们只需要第二个三角形。
1 | int[] triangles = new int[6]; |
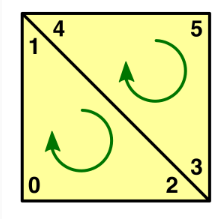
图11 由两个三角形组成的四边形
由于这些三角形共享两个顶点,我们可以将其减少到四行代码,每个顶点索引仅明确提及一次。
1 | triangles[0] = 0; |

图12 第一块正方形面片
我们可以通过将其转换为循环来创建完整的第一行图块。由于我们同时迭代顶点和三角形索引,因此必须同时跟踪它们。我们还可以将 yield 语句移到这个循环中.
1 | triangles = new int[xSize * 6];//6个三角形顶点为一个小正方形循环,所以有xSize* 6 个三角形顶点 |

图13 第一行网格
现在将单循环改为双循环,填充整个网格。注意,移动到下一行需要将顶点索引加一,因为每行的顶点数比图块数多一个。
1 | triangles = new int[xSize * ySize * 6]; |
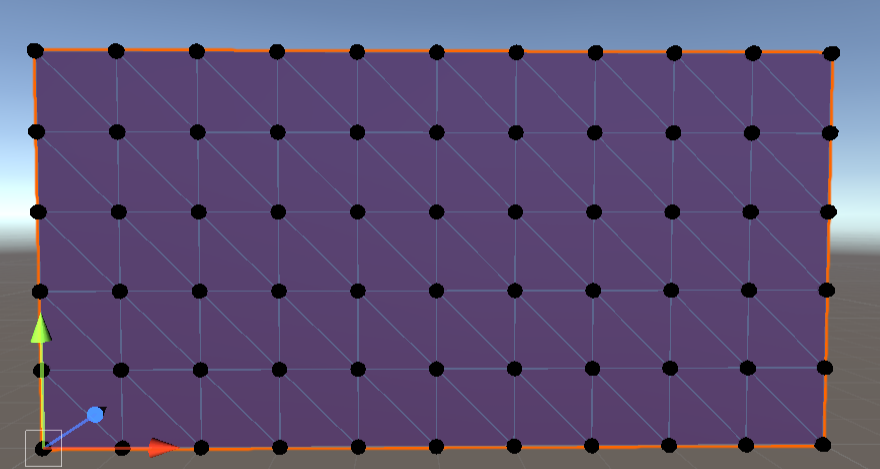
图13 10 * 5网格渲染完成
生成附加顶点数据
我们的网格目前以一种奇怪的方式被照亮。这是因为我们还没有给网格指定任何法线。默认的法线方向是**(0, 0, 1)**,这与我们需要的方向完全相反。
法线如何运作? |
|---|
法线是垂直于表面的向量。我们通常使用单位长度的法线,它们指向表面的外部,而不是内部。 |
法线可以用来确定光线照射到表面的角度(如果有的话)。具体如何使用法线取决于着色器 |
| 由于三角形始终是平面的,因此无需单独提供法线信息。然而,这样做可以起到一定的欺骗作用。 |
| 实际上,顶点没有法线,而三角形有。通过将自定义法线附加到顶点,并在三角形之间进行插值,我们可以假装拥有一个平滑弯曲的表面,而不是一堆平面三角形。只要你不注意网格的锐利轮廓,这种视觉效果就很逼真。 |
法线是每个顶点定义的,所以我们必须填充另一个向量数组。
或者,我们可以让网格根据其三角形自行计算法线。这次我们偷懒一下,直接这样做。
1 | private void Generate () { |
| 如何重新计算法线? |
|---|
该Mesh.RecalculateNormals方法通过找出哪些三角形与该顶点相连、确定这些平面三角形的法线、对它们进行平均以及对结果进行标准化来计算每个顶点的法线。 |

图14 添加法线后
接下来是 UV 坐标。你可能已经注意到,即使网格使用了带有反照率纹理的材质,它目前的颜色也是统一的。这是有道理的,因为如果我们
不自己提供 UV 坐标,那么它们就全为零。
为了使纹理适合我们的整个网格,只需将顶点的位置除以网格尺寸。归一化即可
1 | Vector2[] uv = new Vector2[vertices.Length]; |

图15 uv归一化后正确显示材质
另一种为表面添加更多细节的方法是使用法线贴图。
这些贴图包含以颜色编码的法线向量。将它们应用于表面,
可以产生比单独使用顶点法线更细致的光照效果。
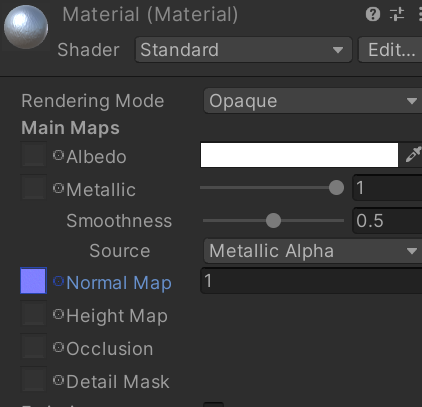

图16 法线贴图材质
将此材质应用于我们的网格会产生凹凸效果,但这是不正确的。我们需要在网格中添加切向量来正确调整它们的方向。
| 切线如何起作用? |
|---|
| 法线贴图定义在切线空间中。切线空间是一个围绕物体表面流动的3D空间。这种方法允许我们在不同的位置和方向上应用相同的法线贴图。 |
| 表面法线代表该空间的向上方向,但哪个方向是正确的呢?这由切线定义。理想情况下,这两个向量之间的夹角为 90°。它们的叉积给出了定义 3D 空间所需的第三个方向。实际上,这个角度通常不是 90°,但结果仍然足够好。 |
| 因此,切线是一个 3D 向量,但 Unity 实际上使用的是 4D 向量。它的第四个分量始终为 -1 或 1,用于控制切线空间的第三个维度的方向——向前或向后。这有利于法线贴图的镜像,法线贴图通常用于具有左右对称性的物体(例如人体)的 3D 模型。Unity 着色器执行此计算的方式要求我们使用 -1。 |
由于我们有一个平面,所以所有切线都指向同一个方向,即向右。
1 | vertices = new Vector3[(xSize + 1) * (ySize + 1)]; |

图17 未用切线坐标(凹凸效果与法线贴图不一致)

图18 使用切线坐标(两次凹凸效果是不一致的)
关于切线后期会补充内容。
绘制圆角立方体
- 创建一个具有无缝网格的立方体。
- 为立方体添加圆边。
- 定义法线。
- 使用子网格。
- 创建自定义着色器。
- 组合原始碰撞器。
合成立方体
处理完二维网格后,下一步就是程序化地生成三维结构。我们来看一下立方体。
从概念上讲,它由六个二维面组成,这些面经过定位和旋转,最终形成一个三维体。我们可以用六个网格实例来实现这一点。
我们的网格位于 XY 平面,朝向负 Z 轴方向。这是立方体的负 Z 轴面。你可以复制它,将其 Y 轴旋转设置为 180°,然后重新定位,使两个面对齐,从而创建正 Z 轴面。
-X 和 +X 面的创建方式相同,但 Y 轴旋转 90° 和 270°。如果需要,您也可以为这些面指定与 Z 面不同的xSize ,但它们的**ySize必须匹配。四个面必须对齐,形成一个闭合的环。
-Y 面和 +Y 面分别由 X 轴旋转 270° 和 90° 构成。它们的x 轴大小应与 Z 面的 x 轴大小一致,y 轴大小应与X 面的x 轴大小一致。
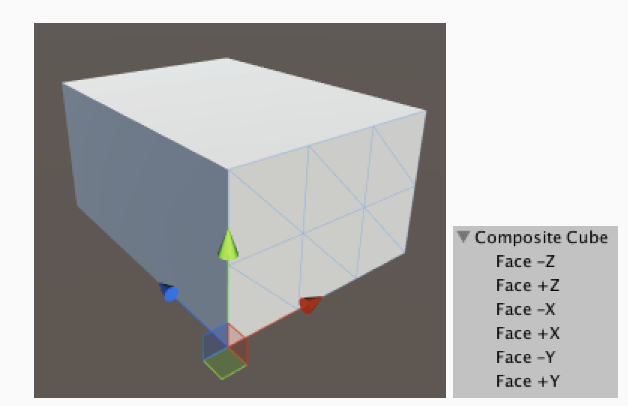
图19 由六个独立网格构成的立方体
这样我们就得到了一个由六个独立网格组成的立方体。虽然看起来不错,可以作为参考,但实际操作起来不太方便。我们可以通过 来组合这些网格
Mesh.CombineMeshes,但不如一次性创建整个立方体。
创建立方体顶点
要创建我们自己的立方体,我们需要创建一个新的组件脚本。让我们利用上一个教程中的一些代码来引导它。
目前唯一的新内容是第三维,所以我们必须添加
zSize。我再次使用了协程和 Gizmos 来帮助可视化正在发生的事情。
1 | using System.Collections; |
在添加立方体的顶点之前,我们首先需要知道它有多少个顶点。
我们已经知道单个面所需的顶点数量。
(#x+1)(#y+1)所以我们只需将这六个面加在一起就可以得到总数。
2((#x+1)(#y+1)+(#x+1)(#z+1)+(#y+1)(#z+1))然而,由于面的边缘相互接触,它们的顶点会重叠,从而导致重复顶点。立方体的每个角顶点数增加了三倍,而其边缘上的所有顶点数增加了一倍。
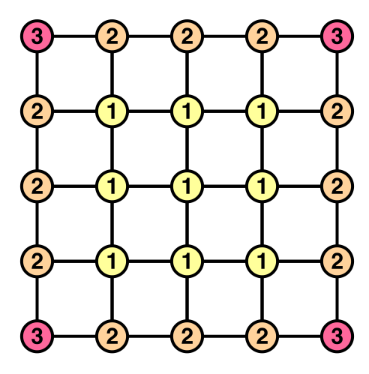
图20 重叠的面顶点
那么我们需要多少个顶点呢?我们按类型来分解一下。首先,我们
有八个角顶点,这很容易理解。然后,我们有十二条边,每个方向四条。由于不包含角,每条边的顶点数等于其对应大小减一。或者,我们可以将其视为四组 X、Y 和 Z 边。
不包含角的十二条边上的顶点:
4(#x+#y+#z−3)其余顶点位于面内。这相当于一个顶点重复的立方体,其尺寸缩小了一半。
中间顶点:
2((#x−1)(#y−1)+(#x−1)(#z−1)+(#y−1)(#z−1))
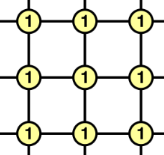
图21 中间顶点
计算顶点个数
1 | /// <summary> |
定位第一面行的顶点与定位网格的第一行完全相同。
1 | vertices = new Vector3[cornerVertices + edgeVertices + faceVertices]; |
接下来会变得更有趣。我们继续从第二个面的第一行开始,依此类推,创建一个由顶点组成的方形环。
这需要循环四次,使用不同的范围和位置。
1 | for (int x = 0; x <= xSize; x++) { |
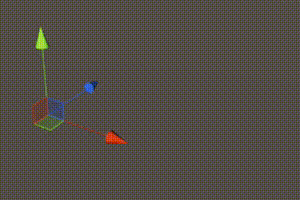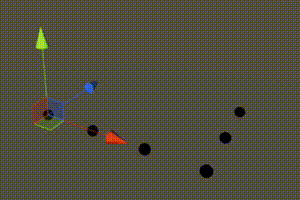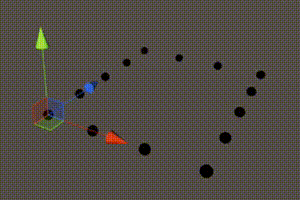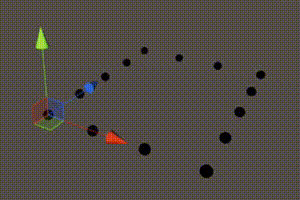
图21 出现底层顶点
通过沿 Y 轴重复放置环,我们可以将其变成立方体高度的完整环绕。
1 | int v = 0; |

图21 外层顶点绘制
之后,我们需要封住顶部和底部。我像普通网格一样填充孔洞。
1 | for (int z = 1; z < zSize; z++) { |

图22 所有顶点位置(无重复)
添加三角形
现在顶点的位置已经正确,我们也熟悉了它们的放置顺序,接下来可以开始处理三角形了。为了做好准备,我移除了协程相关的部分,并添加了分别用于创建顶点和三角形的方法。当然,顶点需要被赋值给网格。
1 | private void Awake () { |
单个四边形的创建与网格完全相同。由于我们最终会在多个位置创建四边形,因此最好为其创建一个方法。
1 | private static int |
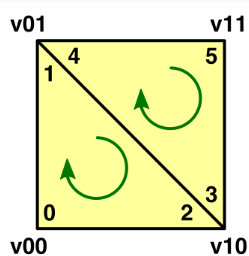
图23 四边形解剖图
与顶点不同,三角形的数量等于六个面的总和。
它们是否使用共享顶点并不重要。
1 | private void CreateTriangles () { |
创建第一个三角形行与创建网格相同。目前唯一的区别是下一行顶点的偏移量等于整个顶点环的偏移量。
1 | private void CreateTriangles() |
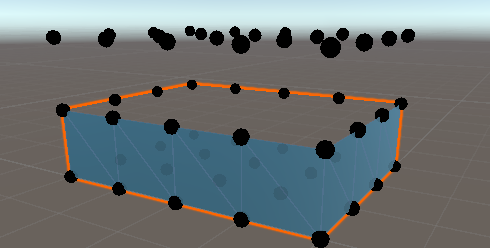
图24 一周面片
要对所有环进行三角剖分,只需再次沿 Y 重复该过程。请注意,每个环之后都需要增加顶点索引,因为我们的环路短了一步。
1 | for (int y = 0; y < ySize; y++, v++) |

图25 外围所有面片
后补
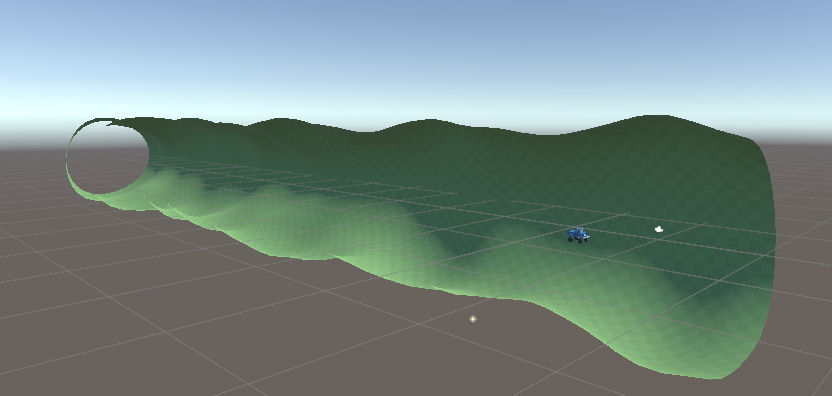
网格实战——利用柏林噪声生成动态地形
生成顶点
我们的需求是类似于一个空心的圆柱体
计算顶点:
(xSize + 1) * (zSize + 1)我们可以把空心圆柱体展开,就是一个长方形,
xSize是围成一圈的网格数,也是长方形的长zSIze是多少圈,也是深度数,也是长方形的宽- 顶点总数即是面积
设置顶点:
要知道顶点就必须知道半径和点对应角度,毕竟我们只知道周长
半径:r =c/2π
角度:angle = x * Mathf.PI * 2f / xSize // x个顶点 平分圆度数
顶点x =sin角 * r
顶点y =cos角 * r
顶点z = z深度值
<img src="https://skymirror-1316984539.cos.ap-beijing.myqcloud.com/Typoraimage-20250730145451738.png" alt="image-20250730145451738" style="zoom:33%;" /><img src="https://skymirror-1316984539.cos.ap-beijing.myqcloud.com/Typoraimage-20250730145748687.png" alt="image-20250730145748687" style="zoom: 50%;" />
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
float radius = xSize * scale * 0.5f;
//顶点索引
int index = 0;
//设置顶点
for (int x = 0; x <= xSize; x++)
{
for (int z = 0; z <= zSize; z++)
{
//根据x的位置来获取角度 知道角度就能得到坐标信息
//每一份平均角度
float angle = x * Mathf.PI * 2f / xSize;// 平分角度数
vertices[index].x = radius * Mathf.Sin(angle);
vertices[index].y = radius * Mathf.Cos(angle);
vertices[index].z = z * scale * Mathf.PI;
index++;
}
}
利用柏林噪声偏移顶点
- 使用 y =a * x +b公式去采样柏林噪声
- 利用向量+ 点为点到这个方向的位移。来偏移顶点
2
3
4
5
6
7
8
9
10
float px = (vertices[index].x * perlinScale) + offset;
float py = (vertices[index].y * perlinScale) + offset;
//需要一个中心点 和当前的顶点做减法然后归一化 再去计算柏林噪声
//这是每个圈的中心点
Vector3 center = new Vector3(0, 0, vertices[index].z);
//计算每个点从中心到点方向的偏移位置,偏移值由waveHight决定 ,偏移方向由柏林噪声决定
vertices[index] += (center - vertices[index]).normalized * Mathf.PerlinNoise(px, py) * waveHight;
index++;
生成网格
需要的三角形索引总数为 xSize * 6 *zSize
法线要向外,所以我们要逆时针连三角形
x表示行索引(从 0 到 zSize)
z表示列索引(从 0 到 xSize)每行有
zSize+1个顶点每行初始顶点为:x * (zSize +1) +z
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
triangles = new int[xSize * zSize * 6]; //一个矩形由两个三角形构成两个三角形一共用6个顶点、
for (int x = 0; x < xSize; x++)
{
for (int z = 0; z < zSize; z++)
{
int baseIndex = x * (zSize + 1) + z;
// 第一个三角形(左下)
triangles[current++] = baseIndex; //0
triangles[current++] = baseIndex + (zSize + 1); //1
triangles[current++] = baseIndex + 1;//2
triangles[current++] = baseIndex + 1;//3
triangles[current++] = baseIndex + (zSize + 1); //4
triangles[current++] = baseIndex + (zSize + 1) + 1;C
}
}